Calculate the factorial of a number in a simple way.

The calculation of the factorial of a number may seem complicated to some, but with the right tools and knowledge, it becomes an accessible and digestible task. In this article, we will explain what factorial is, how to calculate it, and provide you with some practical examples to help you get started with this interesting mathematical operation.

What is a factorial?

The factorial of a non-negative integer ( n ) is represented as ( n! ) and is defined as the product of all positive integers from 1 to ( n ). For example, the factorial of 5 can be expressed as follows:

[ 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 ]

It is important to mention that the factorial of 0 is defined as 1, that is, ( 0! = 1 ).

How to calculate the factorial

The factorial can be calculated either manually or through programming. Below, we'll explain both methods.

1. Manual method

To calculate the factorial of a number manually, simply:

1. Start from the number in question (n).
2. Multiply that number by each positive integer less than it, down to 1.

Example:
To calculate ( 4! ),

• We multiply:
  • ( 4 \times 3 = 12 )
  • ( 12 \times 2 = 24 )
  • ( 24 \times 1 = 24 )
• Thus, ( 4! = 24 ).

2. Method through programming

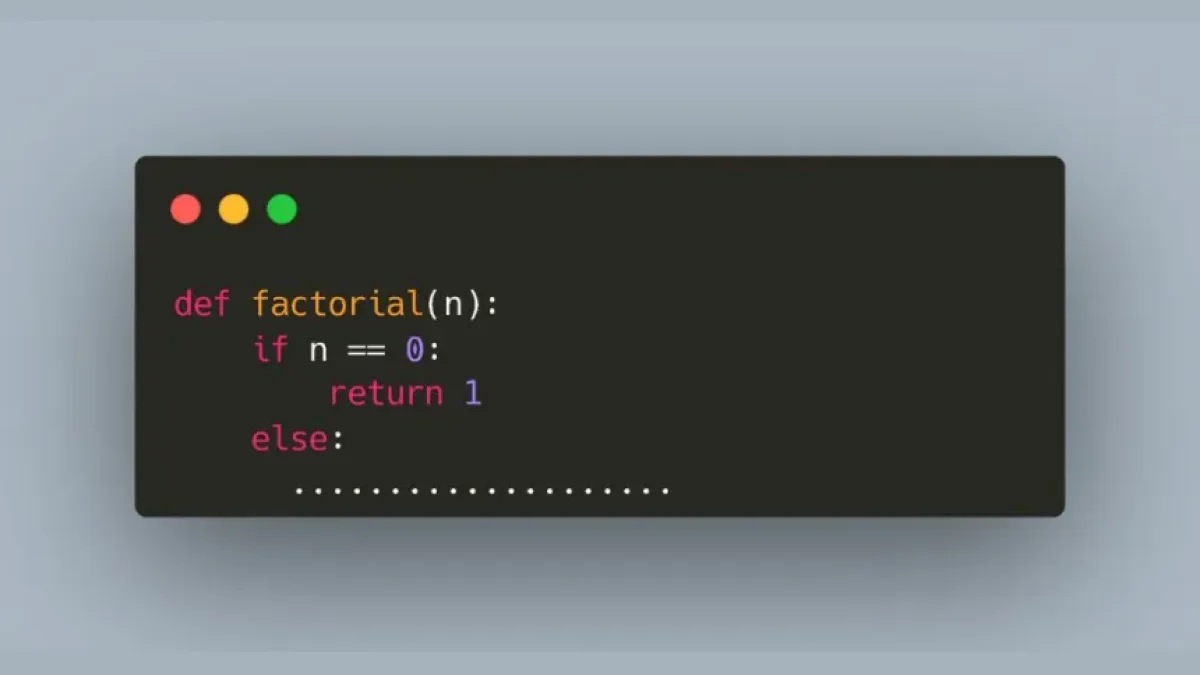
Nowadays, many choose to calculate the factorial using programming languages. Here is an example in Python:

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)

print(factorial(5))  # Output: 120

This piece of code uses recursion to calculate the factorial, a common technique in programming where a function calls itself with a smaller argument.

Applications of the factorial

The factorial has many applications in various areas, particularly in combinatorics and probability. For example:

• Combinatorics: It is used to calculate permutations and combinations. If you want to know how many ways you can arrange ( n ) objects, the result would be ( n! ).

• Probability: It is applied in formulating problems that involve choosing groups of elements.

Conclusions

Calculating the factorial of a number can be both a manual task and a programming activity. With this knowledge, you will have a better understanding of how it is used in mathematics and its practical applications. Feel free to explore more about this and other topics on my blog, where you will find more related articles that will surely interest you.